AVL 树

当要构造二叉树的原有元素序列接近有序时，构造的二叉树会退化成一棵单支树，此二叉树的查找效率也接近于 O(n)，这就失去了构造二叉树的意义（如图1）。为了解决这一问题，苏联科学家 Adelson-Velskii 和 Landis 发明了一种自平衡二叉树，即 AVL 树。

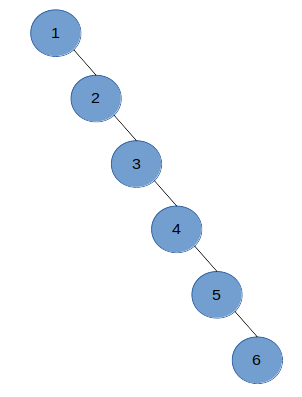图1

AVL 树是一棵具有平衡条件的二叉搜索树，它需要满足树中的每个结点的左子树和右子树的高相差不超过 1。如下图2 中不是 AVL 树，因为根结点 2 的右子树比左子树高 2。图3 中的树为 AVL 树。

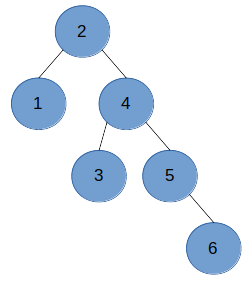图2

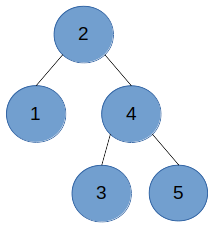图3

AVL 树实现

AVL 树结点比普通的二叉搜索树要多一个高度信息，它在每个结点中记录当前结点的高度信息，这样可以很方便的计算左右子树的高度差，也叫平衡因子，当两边高度差大于 1 时，就需要对树进行调整，以满足 AVL 树的平衡条件。

AVL 树结点定义：

#define AVLTREE_ELETYPE int

// AVL 树结点
typedef struct AVLNode {
    struct AVLNode* parent;    // 父结点
    struct AVLNode* left;    // 左结点
    struct AVLNode* right;    // 右结点
    AVLTREE_ELETYPE data;    //数据值
    int height;    //当前结点高度信息
}tagAVLNode;

结点计算高度的函数：

#define MAX(a, b) \
    (a > b ? a : b)

static int AVLTreeHeight(tagAVLNode* node)
{
    if (node == NULL)
        return 0;
    return MAX((node->left == NULL ? 0 : node->left->height), 
               (node->right == NULL ? 0 : node->right->height)) + 1;
}

创建删除 AVL 结点：

tagAVLNode* AVLTreeMallocNode(AVLTREE_ELETYPE value)
{
    tagAVLNode* node = (tagAVLNode*)malloc(sizeof(tagAVLNode));
    if (node == NULL)
        return NULL;
    node->data = value;
    node->parent = NULL;
    node->left = NULL;
    node->right = NULL;
    node->height = AVLTreeHeight(node);
    return node;
}

void AVLTreeFreeNode(tagAVLNode* node)
{
    free(node);
}

二叉树的旋转

左旋和右旋为 AVL 树恢复平衡条件的基本操作，我们在红黑树实现中也讲过，如下图：

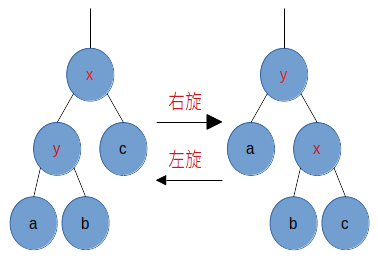
代码实现：

// 左旋
static tagAVLNode* AVLTreeLeftRotate(tagAVLNode* node)
{
    if (node->right == NULL)
        return node;
    tagAVLNode* p = node->right;
    node->right = p->left;
    p->left = node;
    if (node->parent != NULL) {
        if (node->parent->left == node)
            node->parent->left = p;
        else
            node->parent->right = p;
    }
    p->parent = node->parent;
    node->parent = p;
    return p;
}

// 右旋
static tagAVLNode* AVLTreeRightRotate(tagAVLNode* node)
{
    if (node->left == NULL)
        return node;
    tagAVLNode *p = node->left;
    node->left = p->right;
    p->right = node;
    if (node->parent != NULL) {
        if (node->parent->left == node)
            node->parent->left = p;
        else
            node->parent->right = p;
    }
    p->parent = node->parent;
    node->parent = p;
    return p;
}

左旋可以让左子树高度增加，右子树高度减少，右旋可以让左子树高度减少，右子树高度增加，我们就是利用旋转的这一特性来恢复AVL树的平衡的。

执行插入或删除操作后，AVL 树中结点恢复平衡的操作有四种：

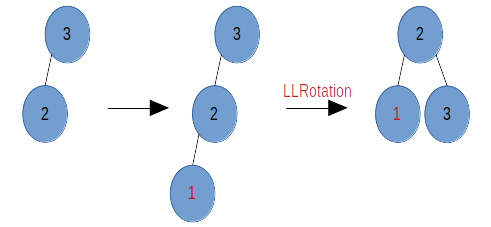
当该结点的左子树比右子树高，且左结点的左子树比右子树高（不低于即可），此时只要进行一次右旋操作即可，我们记为 LLRotation，示例：

如图，当向原树中插入结点 1 时，根结点 3 左子树高为 2，右子树高为 0，结点失衡，因为结点 3 的左结点 2 的左子树比右子树高，因此只需要做一次 LLRotation。

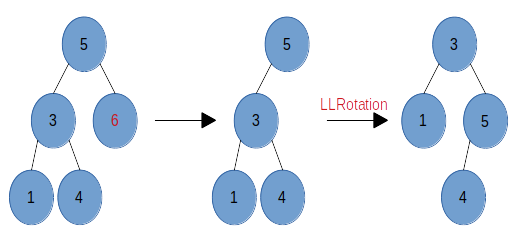
下图中，当从原树中删除结点 6 时，结点 5 的左子树高为 2，右子树高为 0，结点也失衡，因为结点 5 的左结点 3 的左子树不低于右子树，因此只需要做一次 LLRotation。

代码实现：
```
 static tagAVLNode* AVLTreeLLRotation(tagAVLNode* node)
 {
     tagAVLNode* tmp = AVLTreeRightRotate(node);
     node->height = AVLTreeHeight(node);
     tmp->height = AVLTreeHeight(tmp);
     return tmp;
 }
```
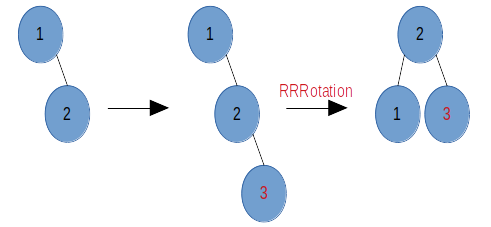
与 1 镜像操作，当该结点的右子树比左子树高，且右结点的右子树比左子树高（不低于即可），此时只需要进行一次左旋操作即可，我们记为 RRRotation，示例：

如图，当向原树中插入结点 3 时，根结点 1 左子树高为 0，右子树高为 2，结点失衡，因为结点 1 的右结点 2 的右子树比左子树高，因此只需要做一次 RRRotation。

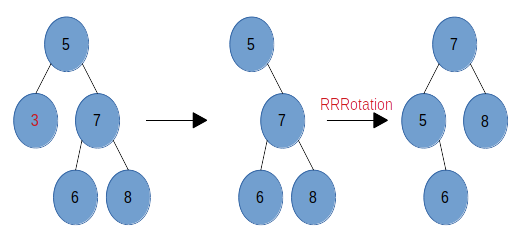
下图中，当从原树中删除结点 3 时，结点 5 的左子树高为 0，右子树高为 2，结点也失衡，因为结点 5 的右结点 7 的右子树不低于左子树，因此只需要做一次 RRRotation。

代码实现：
```
 static tagAVLNode* AVLTreeRRRotation(tagAVLNode* node)
 {
     tagAVLNode* tmp = AVLTreeLeftRotate(node);
     node->height = AVLTreeHeight(node);
     tmp->height = AVLTreeHeight(tmp);
     return tmp;
 }
```
当该结点的左子树比右子树高，且左结点的右子树比左子树高，因为进行右旋时该结点的左结点的右子树会被旋转到右侧树上，所以需要两次操作，先对该结点的左结点进行一次左旋，使其左结点的左子树的高不低于右子树，然后再对该结点进行一次右旋，我们记为 LRRotation，如图：

当在树中添加或删除结点后形成图中最左边的树形状时，此时结点 10 的左子树高为 3，右子树高为 1，高度失衡，但是因为结点 10 的左结点 6 的左子树高低于右子树，所以先对结点 10 的左结点 6 进行一次左旋（RRRotation），然后再对结点 10 进行一次右旋（LLRotation），此时结点达到平衡。

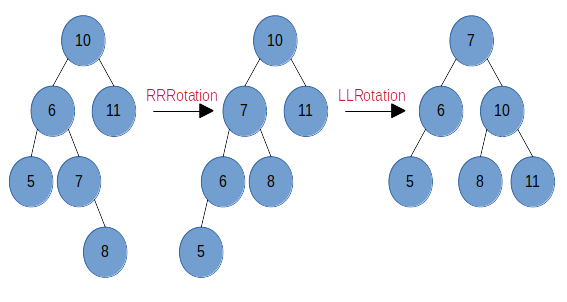
代码实现：
```
 static tagAVLNode* AVLTreeLRRotation(tagAVLNode* node)
 {
     AVLTreeRRRotation(node->left);
     return AVLTreeLLRotation(node);
 }
```
与 3 镜像操作，当该结点的右子树比左子树高，且右结点的左子树比右子树高，因为进行左旋时该结点的右结点的左子树会被旋转到左侧树上，所以也需要两次操作，先对该结点的右结点进行一次右旋，使其右结点的右子树的高不低于左子树，然后再对该结点进行一次左旋，我们记为 RLRotation，如图：

当在树中添加或删除结点后形成图中最左边的树形状时，此时结点 5 的左子树高为 1，右子树高为 3，高度失衡，但是因为结点 5 的右结点 8 的左子树高于右子树，所以先对结点 5 的右结点 8 进行一次右旋（LLRotation），然后再对结点 5 进行一次左旋（RRRotation），此时结点达到平衡。

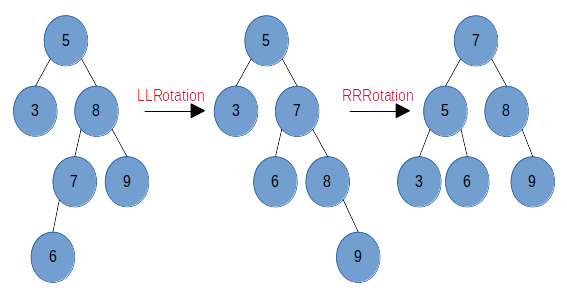
代码实现：
```
 static tagAVLNode* AVLTreeRLRotation(tagAVLNode* node)
 {
     AVLTreeLLRotation(node->right);
     return AVLTreeRRRotation(node);
 }
```

AVL 树的插入

有了 AVL 树结点恢复平衡的方式，我们可以来进行 AVL 树结点的插入和删除。这里我们都用的递归的方式来求解。

插入结点时，先根据插入的值来确定插入结点的位置，创建结点并插入后从插入点向上依次判断结点是否满足平衡条件，如果不满足则根据四种旋转方式来调整：

tagAVLNode* AVLTreeInsert(tagAVLNode* root, AVLTREE_ELETYPE value)
{
    if (root == NULL) {
        return AVLTreeMallocNode(value);
    } else if (root->data > value) {
        root->left = AVLTreeInsert(root->left, value);
        if (root->left != NULL)
            root->left->parent = root;
        root->height = AVLTreeHeight(root);
        if (AVLTreeHeight(root->left) - AVLTreeHeight(root->right) > 1) {
            if (root->left->data > value)
                return AVLTreeLLRotation(root);
            else
                return AVLTreeLRRotation(root);
        }
    } else if (root->data < value) {
        root->right = AVLTreeInsert(root->right, value);
        if (root->right != NULL)
            root->right->parent = root;
        root->height = AVLTreeHeight(root);
        if (AVLTreeHeight(root->right) - AVLTreeHeight(root->left) > 1) {
            if (root->right->data > value)
                return AVLTreeRLRotation(root);
            else
                return AVLTreeRRRotation(root);
        }
    } else {
        printf("node has exist!\n");
    }
    return root;
}

AVL 树的删除

AVL 树删除结点时需要先查找到该结点，然后分几种情况来删除，当该结点为叶子结点时，直接删除该结点。当该结点只有一个孩子时，将该结点直接替换成它的孩子结点，其孩子结点必定是叶子结点，直接删除其子结点。当该结点有两个孩子时，我们用它的前驱或后继来替换它，然后删除它的前驱或后继。前驱结点可以通过查找它的左子树的最大值，后继结点可以通过查找它的右子树的最小值来实现。这里我们用后继实现。

代码实现：

tagAVLNode* AVLTreeFindMin(tagAVLNode* root)
{
    if (root == NULL)
        return NULL;
    if (root->left != NULL)
        return AVLTreeFindMin(root->left);
    else
        return root;
}

tagAVLNode* AVLTreeFindMax(tagAVLNode* root)
{
    if (root == NULL)
        return NULL;
    if (root->right != NULL)
        return AVLTreeFindMax(root->right);
    else
        return root;
}

// 删除 AVL 树结点
tagAVLNode* AVLTreeDelete(tagAVLNode* root, AVLTREE_ELETYPE value)
{
    if (root == NULL)
        return NULL;
    else if (root->data > value) {
        root->left = AVLTreeDelete(root->left, value);
    } else if (root->data < value) {
        root->right = AVLTreeDelete(root->right, value);
    } else {
        if (root->left != NULL && root->right != NULL) {
            tagAVLNode* node = AVLTreeFindMin(root->right);
            root->data = node->data;
            root->right = AVLTreeDelete(root->right, node->data);
        } else if (root->left != NULL) {
            root->data = root->left->data;
            root->left = AVLTreeDelete(root->left, root->left->data);
        } else if (root->right != NULL) {
            root->data = root->right->data;
            root->right = AVLTreeDelete(root->right, root->right->data);
        } else {
            AVLTreeFreeNode(root);
            return NULL;
        }
    }

    root->height = AVLTreeHeight(root);
    if (AVLTreeHeight(root->left) - AVLTreeHeight(root->right) > 1) {
        if (AVLTreeHeight(root->left->left) >= AVLTreeHeight(root->left->right)) {
            return AVLTreeLLRotation(root);
        } else {
            return AVLTreeLRRotation(root);
        }
    } else if (AVLTreeHeight(root->right) - AVLTreeHeight(root->left) > 1) {
        if (AVLTreeHeight(root->right->right) >= AVLTreeHeight(root->right->left)) {
            return AVLTreeRRRotation(root);
        } else {
            return AVLTreeRLRotation(root);
        }
    }
    return root;
}

AVL 树的遍历

AVL 树是一棵特殊的二叉树，其遍历同二叉树的遍历相同，具体过程不再缀述，请参考二叉树的四种遍历方法

参考：

<数据结构与算法分析-C语言描述> P4